Hi, I’m Rick Hoskinson, an engineer on the League of Legends Core Gameplay Initiative, and I’m here to talk about how we gave ourselves the power to turn back the hands of time in League of Legends. In this series of blog posts, I hope to give you a glimpse of what that work looked like, juicy technical challenges and all.

In this third post, I’ll cover the single largest area of effort required to achieve determinism: the unified clock. You’ll learn how we measured time in game, identified problems in LoL time APIs, designed a future-proof time system for LoL, and dealt with implementation challenges.

Measuring Time in Games

High precision clocks are the metronomes of modern games. They provide the mechanism by which time in the game passes in real-time, regardless of the speed of the hardware on which it is played. To understand why we need high-precision clocks, it’s first important to understand how the frame-quantized simulations used in most real-time video games work.

Game simulations are architected by quantizing a continuous process into a series of frames. The primary value that feeds into most per-frame calculations is not the total game time, but rather the time it took to process the previous frame. This time value (interchangeably referred to as “delta time” and “elapsed time”) is the current frame’s timestamp minus the previous frame’s timestamp.

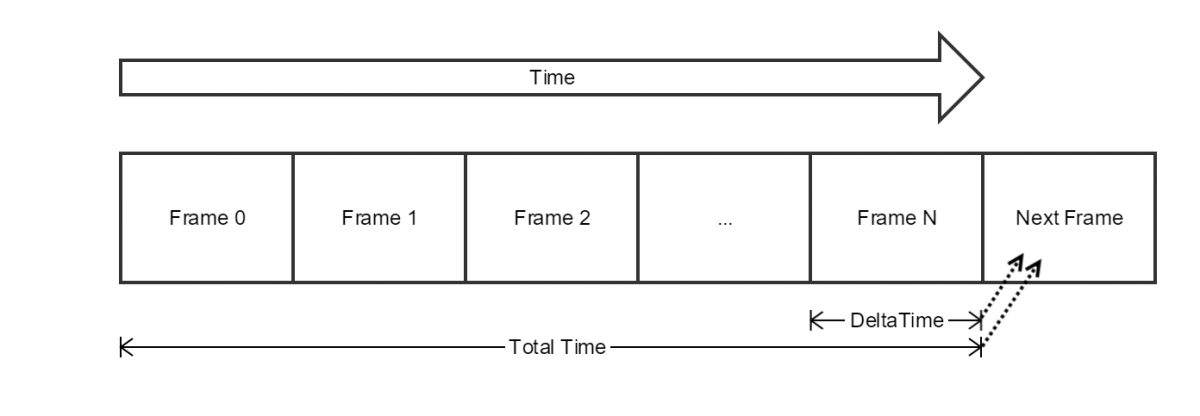
Physical game objects are updated each frame using elapsed time. As long as the quanta of time is small enough, the game creates the illusion of continuous, physically plausible motion.

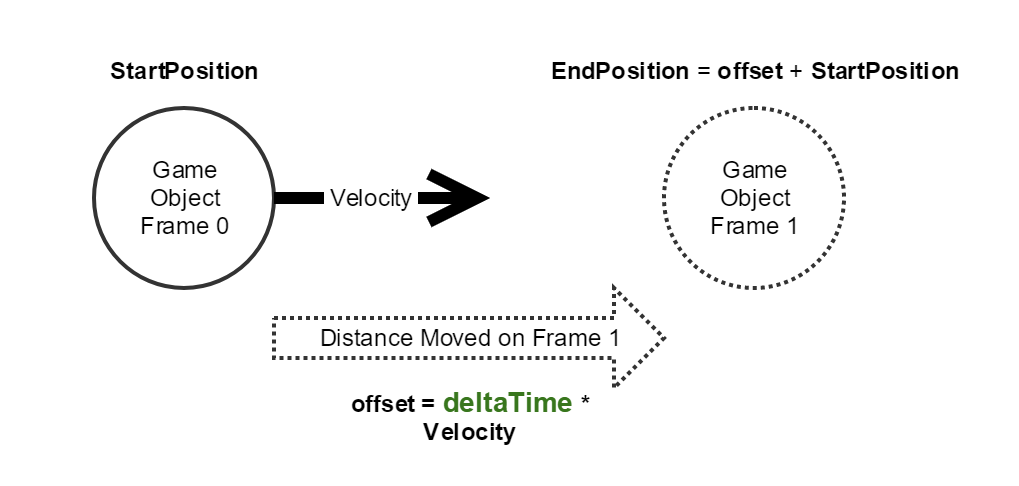
In League, elapsed time and absolute time are both sampled at the start of each frame, just before gameplay processing begins. We tend to avoid using sub-frame time, as it tends to not be meaningful when inputs and outputs are limited to the framerate of the game simulation. It also creates problems with determinism, which we covered in Part 2 of the determinism devblog series.

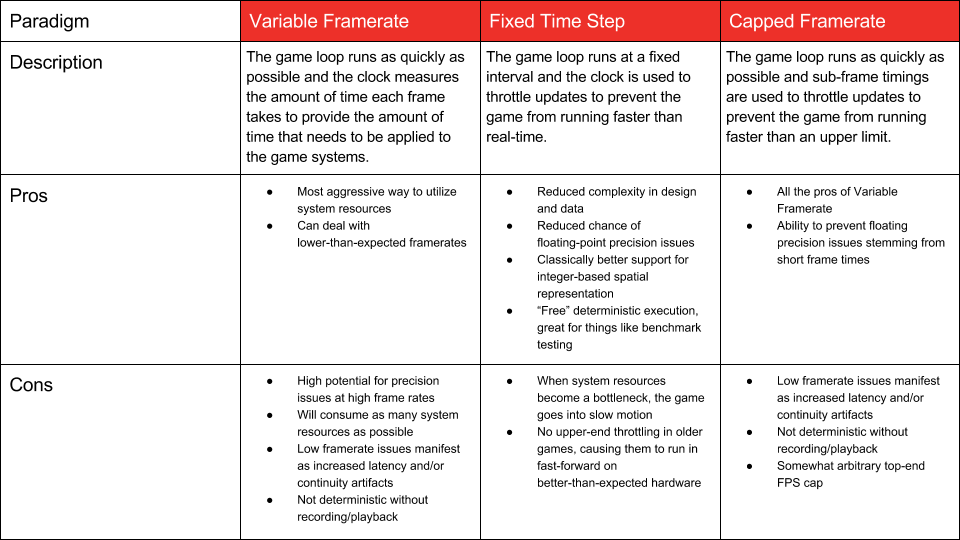
There are a few different paradigms for controlling the simulation frame rate of a game. I’ve simplified this table to avoid the intricacies of task-based multithreading, as League is predominantly a single-threaded game.

As far back as mid-2015, long before I’d started thinking about determinism, I had found some fairly daunting issues with the high-precision clocks and timers APIs in LoL. I wrote an implementation specification (in the form of a Riot Request for Comment) that would become a major portion of the overall determinism effort that started in earnest in early 2016. The refactoring of existing League clocks into what would be called the “Unified Clock” represented the largest portion of the determinism effort, but also yielded one our most impactful improvements in code quality.

Problems in LoL Time APIs

Issue 1: Many Clocks, Many Implementations

Long before we proposed a serious attempt at server determinism, we’d already identified a problem with our existing high precision clocks. “Clocks” is the correct term here, as we had a plurality of them. When we started the determinism project, we had 8 clock instances with 6 unique implementations. Each implementation captured some subset of clock functionality utilized by the game but none had a complete implementation that we could use in all parts of the League game client and server.

The major problem was that this would add a huge amount of complication around time measurements leaking into a deterministic playback of the game. We also noticed several degenerate behaviors relating to clock usage - the worst being related gameplay systems sampling time from different clocks. Most of our 8 clock instances were initialized at different times in the game, so they would each give subtly different numbers when measuring absolute time. This meant many game systems had a great deal of code dedicated to translating the time-domain of one clock measurement into another. This complicated the code and proved to be the source of a few subtle bugs we fixed during the creation of a new clock system.

Issue 2: Floating Point Precision

Another major problem with most implementations of our low-level clocks was that they used 32-bit floating point time accumulators, which are imperfect approximations of real numbers. Single-precision floats can only represent an extremely limited amount of detail in 32-bits. Most physical representations of game objects use single-precision floats for performance and historical reasons. The vast majority of the time this use is perfectly fine within a game, but some specific systems - especially those with time representations - can be highly sensitive to detail loss from floating-point precision issues.

Floating-point precision in games is a large topic. If you’re working on game engine code at any depth, I highly recommend a wonderful series of blog posts by a former colleague of mine. Bruce Dawson’s posts give great insight into real-world pitfalls with floating point numbers.

For the purposes of this blog, we can summarize the problem as: Adding or subtracting small floating-point numbers to large ones leads to precision problems. In the simplest case, this issue causes problems when adding frame delta times (usually less than 0.033 seconds) to a variable representing total game time (which can be north of 4000.0 seconds). The small delta time details are truncated as they’re summed into a large, accumulated floating point number. As this detail is lost, total game time drifts away from real-time. When these imprecise numbers are then fed back into other lossy mathematical operations, they can result in catastrophic in-game problems, such as game objects skipping around, moving erratically, or glitching out in other ways.

This problem was compounded by the various clock implementations present. Different clock instances would end up running at different rates as the game went on. We even had specialized code in the game that applied magic number multipliers to correct for drift between clock instances.

Sidebar Note

We do still see precision issues (that many mistake as network latency) when client framerates are uncapped and allowed to run extremely high. Capping one’s frame rate (or using VSync) to keep framerate at 144Hz or less will generally result in a smoother gameplay experience than a game running at 200+ Hz framerates. Though it does appear that gameplay artifacts at extreme framerates have been somewhat reduced, some issues are still present in the current patch of this writing. If you’re running at over 144Hz and have been noticing visual glitches, try capping your framerate and see if they are still present.

Issue 3: Clock Synchronization

Many modern games rely on accurate, high-precision synchronization of clocks between the client and server. This creates numerous opportunities to simplify gameplay implementation and apply a variety of latency compensation techniques. Aurelion Sol is an example of a champion that relies on network-synchronized clocks to accurately synchronize his long-lived orbs between the client and the server.

One of our five clocks did handle synchronization fairly well, though it was a very simple implementation that biased the offsets between client and server. To enable more gameplay systems to rely on these numbers, we also wanted to develop a clock synchronization mechanism that would converge quickly and offer single-millisecond accuracy, which opens up doors in the future for improved latency compensation.

Designing a Future-Proof Time System for LoL

I won’t speculate on how the codebase ended up with so many implementations of clocks, but it was clear to us that we’d see some fairly major productivity gains by creating a centralized, robust, precise, and easy-to-understand time system. I dubbed this system the “Unified Clock” back when I penned the original implementation specification, though nowadays we refer to it as “the clock” in League of Legends.

Before development began we listed all the features and capabilities we knew we’d want. This included:

• A single API accessible from any part of the codebase

• Discoverable, self-documenting API design

• Fast-converging, sub-millisecond-accurate network clock synchronization

• Support for multiple clock instances with different game behaviors

• An API for child timers controlled by the behavior of their parent clocks

• Support for network replicated pause and time scale controls

• Support for fixed time steps

• Support for recording/playback of variable frame-times

API Design

This design took some time to mature, but I’m pretty happy with the results. I feel like clocks are absolutely one place where variable- and method-naming are critical to code comprehension. I also wanted to avoid past mistakes by creating a complete, authoritative API that would naturally dissuade developers from writing their own clocks on an ad-hoc basis.

I built the clocks around a central clock manager type that the user of the API could access through a variety of API facades. The facades consist of separate interfaces for read-only clock access and read/write clock controls.

We chose verbose (some might say pedantic) conventions for naming, and we avoided template code to simplify debugging and static comprehension for developers using the C++ headers as documentation.

An example from our read-only facade looks somewhat like this (truncated for brevity):

class FrameClockFacade
{
public:
   //Get the time elapsed since last frame
   float GetElapsedFrameTimeSecs() const;
   double GetElapsedFrameTimeSecsDbl() const;

   //Current time at the start of this frame since the clock was started
   float GetFrameStartTimeSecs() const;
   double GetFrameStartTimeSecsDbl() const;
 
   /*
       etc.
   */
};

A programmer should have no questions about using these methods that couldn’t be rapidly ascertained from the header details. Compare that to this example of a clock that we replaced:

class IClock
{
public:
   float GetTime();
   float GetTimeDelta();

   /*
       etc.
   */
}

While at first glance the second code block seems simpler, the lack of context routinely led engineers to use functions like this incorrectly. In this specific example there are no units, indications of whether GetTime() refers to absolute or elapsed time, or details on whether GetTime() is frame time or instantaneous time.

During the creation of the new clock, we found numerous subtle issues like milliseconds being treated as seconds and frame-elapsed times being treated like absolute times. The bugs from these issues might then be hidden by the usage of other clock instances, which led to even more subtle in-game issues as time domains became mismatched between different sources of time.

Internal Representation

As hardware and OSes have changed over time, the resolution and accuracy of the underlying time systems has evolved. To keep up with these trends, OS developers are providing flexible time APIs instead of simply returning an estimate in seconds, nanoseconds, or whatever the lowest precision unit of the day happens to be.

On Windows, we use QueryPerformanceCounter to get a count of integer-based “ticks” which must then be related back to real time by also querying tick frequency using QueryPerformanceFrequency. On MacOS, we use mach_absolute_time, which has the corresponding query function mach_timebase_info. Ticks are awkward to use, since they change in frequency from PC to PC so a tick count on the server can’t be usefully compared to a tick count on a client. However, internally we only store ticks in the clock classes as measurements of time as they represent the most accurate quanta of time we can obtain from the OS timing APIs we’ve chosen. To minimize errors from conversions, we only convert back to floating point or integer representations of time at the time of the API call.

We can’t stop a user of the API from creating a long-lived floating-point variable that accumulates an absolute time from frame-elapsed time samples, which can cause long-term precision issues in game. However, we can try to mitigate this pattern by providing convenient timer classes that wrap around the clocks and an internal, high-precision tick count.  

Our timers do have a bit more implementation complexity than a simple counter due to the fact that they can be slaved to a parent clock to take advantage of its global controls. A child timer of a clock that gets paused will not advance until the parent pause is cleared. The same principle goes for other parent properties such as fixed time steps and clock scaling. These timers then enable engineers to focus their efforts on more sophisticated problems than simply providing consistent gameplay timings.

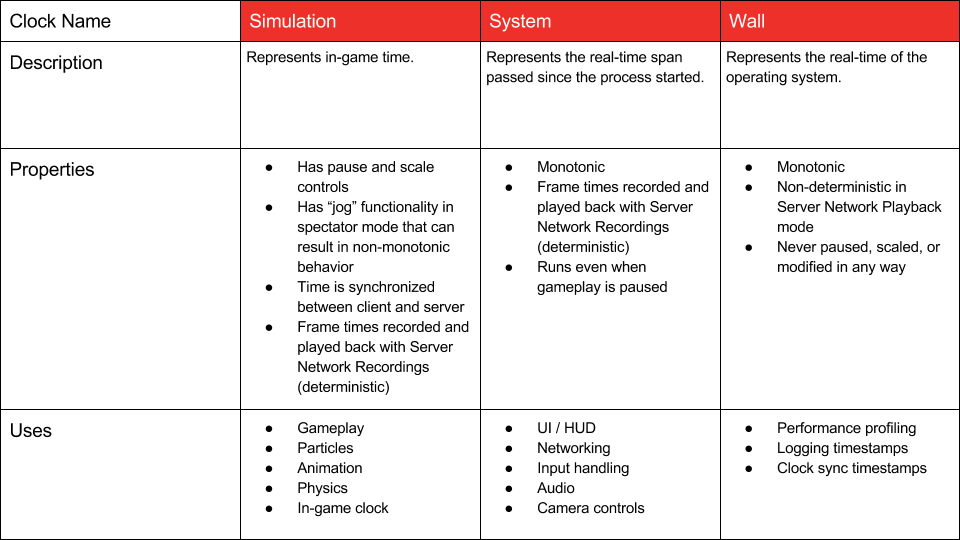
Clock Instances

Different game systems expect different behaviors from the underlying time sources. A good example of this is the clock used to drive UI animations vs. the source of time used to increment the game state. If one pauses the game state, there may be UI elements that require an unpaused clock to complete UI animations so that menus are still interactive.

A perfectly valid implementation for this is to have a single, constantly incrementing clock and timer instances that govern execution of individual game systems. However, I decided that I wanted to favor minimizing the number of “global” timers in the game, and instead reserve timers for more specialized measurements. The result was the following array of time sources.

I avoided using singletons to contain the individual game clocks to facilitate easier functional tests. I wanted master and replicated (synchronized) clocks in the same process so I could easily test network clock sync using a virtualized network. This worked out extremely well as I was able to simulate specific network conditions and reproduce one-off bugs using a test network interface without the overhead of comparing results from two separate applications (be it test applications or the actual League client and server.) Instead, I made a game-specific global singleton that contained all of my clock instances with global functions to simplify access to the individual clocks. Here’s an example of what this could look like:

pos =  RiotClock::Simulation().GetElapsedFrameTimeSecs() * vel + pos;

That callsite may look egregious and maybe it has gone a little far. I may eventually abridge the calling convention to increase readability. However, I will take the previous example any day over the following:

pos =  getTime() * vel + pos;

Some game engines I’ve seen solve this by passing frame-elapsed times or start times to update functions, which makes the caller of an update function responsible for knowing what flavor of time the game object should be receiving. I don’t like this pattern because, as a reader of code, I need to trace back to the update’s callsite to understand what time domain I’m operating in. It also means developers need to add extra parameters to every update-style function call in the game.

Clock Sync

Clock sync is a well-trod topic, and I won’t go too far into the general details here. If you’re interested, the Wikipedia article on the Network Time Protocol is a great place to start. If you really want to go deep on NTP and understanding computer clocks in general, Computer Network Time Synchronization by David L. Mills is a wonderful and highly detailed reference for all things time sync.

The main concept from NTP that we utilize is the idea of an offset which is calculated by time-stamping our client clock sync requests and the responses from the server.

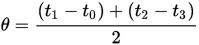
The LoL implementation starts to diverge from NTP beyond the offset since our usage scenario is very different than typical PC or mobile device synchronization. We need to converge quickly on a usable offset, ideally within the time between the client connection and the end of the in-game loading screen. We also need to synchronize high-precision clocks and attempt to get our clock accuracy within a few milliseconds at worst.

To facilitate this, we start by sending back-to-back sync requests from the client until we’ve received enough valid sync events to establish a preliminary offset. We also measure the network delay (calculated using our same four timestamps, only using the equation 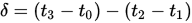). The network delay of each event is used for outlier detection. I establish a reference delay by averaging delay events, obtaining a standard deviation, and then rejecting events that are off by a multiple of standard deviation.

Once we have enough valid synchronization events, we can establish an average offset. After the offset is established, we slow the rate of synchronization to a fixed interval that increases proportionally to the amount of variance we see in the offset. We use filters to deal with drift and delay changes over the course of the game.

The next tricky bit is dealing with the fact that the clock system has support for more than one synchronized clock and these clocks may be paused or scaled. Typical NTP-style systems attempt to return a server time with the expectation that the client clock is acting like a “wall” clock, but we wanted to take this a step further and deal with sync artifacts arising from variable network and process latency in replicated pausing/scaling. This means that if we have a delayed “unpause” packet, the delay is accounted for and the client will apply additional velocity to catch up.

Once we have a solid estimate of server time, we want to ensure that the client clock instance converges on this time reliably. We don’t simply snap to a time, as that can create jarring in-game artifacts. Instead we gradually filter the client clock times to slowly approach server time. This means we very slowly - almost imperceptibly - speed up or slow down individual frames to re-synchronize the client clock. We allow the client clock to run 1.3 times faster or slower to “catch up” with the server clock, which we found to be a good tradeoff between convergence time and visual artifacts. In most cases, this means time feels slightly slowed down or sped up.  

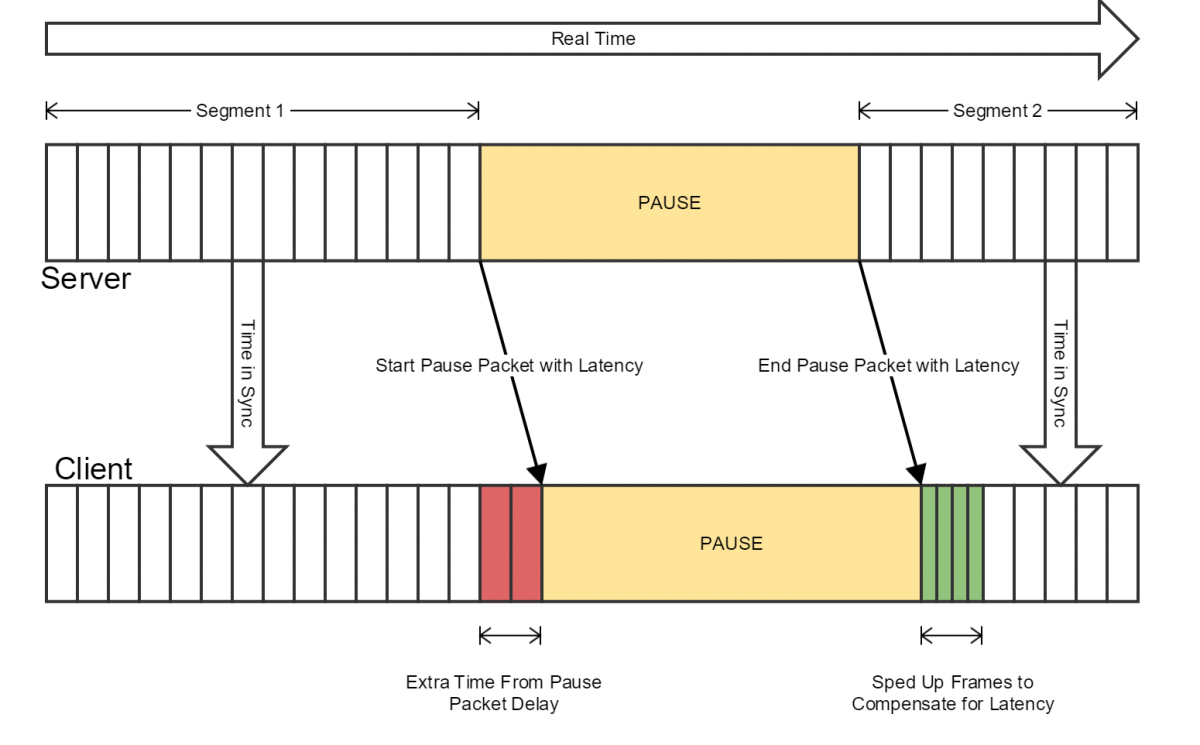
In practice, after the initial synchronization, the client clocks tend to re-sync to changes in offset in one frame, and rarely hit the 1.3x multiplier for time acceleration or deceleration. This has been more than sufficient for hiding artifacts due to the relatively subtle drift that we’ve been able to detect in real-world hardware.  

We also have to deal with the fact that, few systems in the game were designed to deal with non-monotonic times (meaning time that can go backwards). So if our filters tell us server time is running behind client time for some reason, we need to ensure we never go into negative frame-elapsed time. If we do detect this situation, we clamp the elapsed time to 0 and apply the remainder of the negative value to future frames until the client can resume a normal clock speed.

The synchronization and filtering code is the most complex part of the entire clock system, as it needs to balance mathematical rigor with player experience. I even included a little ASCII skull-and-crossbones at the start of the implementation to remind future devs to read the notes and comments in the file before altering the code.

Implementation Challenges

Rolling Out High Risk Changes

Chief amongst our implementation challenges was deciding how to roll out a change as fundamental and risky as replacing and potentially changing the behaviors of every time access in the game. There were hundreds of callsites in the LoL codebase that had to be modified to point to the new clock systems.

To facilitate this change, we started treating the existing clocks as adaptors that would allow us to dynamically switch between the existing clock calls and the new system. Each callsite would remain the same, but we added the capacity to toggle between the underlying source of truth. We still had to pick our battles though, and we rolled the clocks out in a long series of internal testing, beta testing, and finally a region-by-region rollout to live environments. This required months of time and a huge amount of logistical support from our quality assurance department.

Spectator Mode and Monotonicity

Many systems in the game relied on specific clocks’ idiosyncrasies. The main issue we encountered was in our spectator system. The spectator mode of the client is the only one in which the game rewinds. This happens every time a player uses the timeline controls to jog the playback to an earlier time.

Nearly every previous clock in the game was purely monotonic, meaning it only ever moved forward. Most gameplay systems had been coded to rely on monotonic clock behavior. Those systems addressed the spectator problem with a huge amount of complex, one-off code to transform from the monotonic clock’s time domain into the game time we show in the upper right corner of the LoL HUD.

Other game systems simply didn’t play nice with the new “shared” behavior. This meant a long period of bug fixing as we found and fixed systems that had never before had to deal with non-monotonic clock behaviors. One of the most blatant problems occurred in the particle system, which had the nasty property of not cleaning up emitters when using the spectator to rewind to a time before the emitter was created.

The @#$^@^% Pause System

The final problem I left for the end of the clock replacement process was to make the in-game gameplay pause systems (found in custom games) work in tandem with the new low-level clock. This sounded fairly easy in my head, so I’d left it for last. However, I’d severely underestimated how fundamental the old clock behaviors around pause were to the game’s spectator mode.  

The entirety of our spectator streaming technology was based on the old pause behavior which would pause some clock instances but not others. Resolving the resultant issues required downright scary changes to low-level streaming/buffering code as well as to the spectator playback loop itself. What I estimated at a couple weeks of work became a two month development quagmire as we continuously found edge-case regression bugs that would require high-risk changes to correct.

Fixing the Time Step

One of the most challenging strategic decisions when dealing with server determinism was the question of whether to maintain the existing capped framerate or switch to a fixed framerate implementation.

Moving to a fixed frame time is, in some ways, a more satisfying solution to the determinism problem as we remove frame time as an input. Once frame time is a hard-coded value, numerous doors open for deterministic testing, optimization, and simplification. These value adds are generally small and situational, but they do add up to a more stable, knowable game simulation.

However, fixed frame rate problems impact player experience, and it came down to a fundamental question: If the LoL server has a temporary performance issue, is it better to reduce refresh rate thereby increasing latency -or- put the game into slow motion?

There is precedent for both models of dealing with performance issues found in classical and modern videogames. The primary reason we stayed with capped framerates was simple: the existing behavior is well established for long-time players of League of Legends. We do not deviate from real-time, and given the rarity of performance issues at the server process level, slowdown would likely be more jarring than temporary additional latency, for which we have existing compensation measures in place.

A secondary consideration was how to properly synchronize client clocks when a slowdown is detected. League does not use the lock-stepped, synchronized peer-to-peer networking common in sports, fighting, and traditional real-time strategy games. In such games, a slowdown on one peer can cause a slowdown or freeze on all of the other peers in the game. However, we would have had to make special compensation for this in the synchronized Simulation Clock, which is a solvable but non-trivial problem.

In the end, we went with a playback recording solution, which reduced the impact on our delivery schedule and allowed us to ship Project Chronobreak at the start of Season 7.

Conclusion

I hope this post gives some insight into how a seemingly simple function like measuring time end up being one of the key refactors necessary for a sustainably deterministic game server. Though it required a considerable amount of time to accomplish, the process of creating a unified clock has allowed us to greatly increase overall LoL code quality. Our game engineers are more productive and are able to create robust, latency tolerant gameplay systems.

The next article will be the final post in the determinism dev blog series. We’ll cover the systems we used to measure determinism and show the detective work that goes into tracking down a divergence.

I want to end with a big “thank you” to all those sticking with me through this series.

For more information, check out the rest of this series:

Part I: Introduction
Part II: Implementation
Part III: Unified Clock (this article)
Part IV: Fixing Divergences